解答：90°
角アは４５°とすぐにわかりますが、角イと角ウの角度をそれぞれ求めようとしても、この問題は解けません。そこで工夫して、角イと角ウの合計が求められるようにします。

解説その１


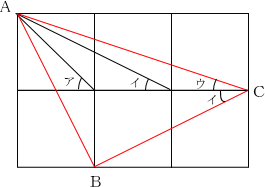
角ウの下に角イが来るように、三角形ＡＢＣをつくります。この三角形は、辺ＡＢと辺ＢＣの長さが等しく、かつ角ＡＢＣは角イの三角形の２つ角の合計なので、直角となります。したがって、三角形ＡＢＣは直角二等辺三角形であることがわかり、その底角である角ＢＡＣおよび角ＡＣＢはそれぞれ４５°となります。ゆえに、角イと角ウの合計は４５°。これに角アの４５°を足して９０°となります。

解説その２（中学３年で習う三角形の相似条件を使った解き方。）
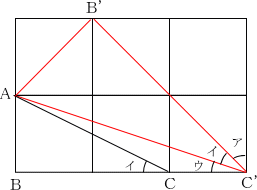
下の図のように、角ウがある正方形に対角線を引き、それをさらに伸ばして三角形AB'C'を作ります。この三角形は、辺AB'：辺B'C'の比が1：2で、かつ角AB'C'は直角です。また三角形ABCも辺AB：辺BCの比が1：2で、かつ角ABCは直角なので、三角形の相似条件のうちの「2辺の比とその間の角が等しい」が成り立ちます。ゆえに三角形ABC∽三角形AB'C'となり、角ACB＝角AC'B'＝角イが導かれるので、角ア、角イ、角ウの合計は90°となります。



解説その３
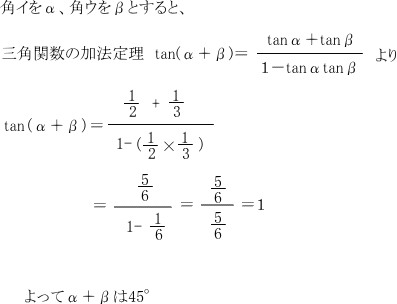
高校生以上でしたら、角イと角ウの合計は、次のようにして簡単に求めることができます。