答え：２０c㎡。
答えは一つですが、答えにたどり着くまでの方法はいくつもあります。みなさんも一緒に考えて見ましょう。



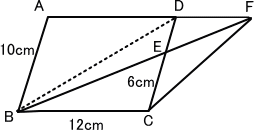
解き方１……BD間に線を引くと、三角形BCDと三角形BCFはどちらもBCを底辺とする同じ高さの三角形となるので、面積は等しい。この二つの三角形は三角形BCEが両方に共通しているので、それを除いた三角形BDEの面積＝三角形CEFの面積となる。平行四辺形ABCDの面積が100c㎡なので、三角形BCDの面積はその半分の50c㎡。点Eは辺CDを6：4に分割しているので、三角形BCEの面積：三角形BDEの面積も6：4になることから、三角形BDEの面積を求めると、50÷10×4＝20。よって三角形BDEの面積＝三角形BCFの面積は20c㎡。

解き方２……「解き方１《と同じようにBD間に線を引く。三角形BCDと三角形BCFは同じ面積となる。三角形BCEの面積は、三角形BCDの10分の6なので、50÷10×6＝30。三角形BCFから三角形BCEの面積をひけば三角形CEFの面積が求められるので、50-30＝20　よって三角形CEFの面積は20c㎡。

解き方３……三角形BCDの面積は平行四辺形ABCD（100c㎡）の半分なので50c㎡。DE：EC＝4cm：6cm＝2：3より、三角形BDEの面積：三角形BCEの面積＝2：3なので、三角形BCE＝30c㎡。三角形BCEと三角形FDEは相似なので、CE：ED＝6cm：4cm＝3：2より、BE：EF＝3：2。よって、三角形BCEの面積：三角形CFEの面積＝3：2なので、三角形CFEの面積は20c㎡。

解き方４……三角形DEFと三角形CEBは相似なので、DE：EC＝4cm：6cm＝2：3より、DF：BC＝2：3。BC＝12cmより、DF＝8cm。三角形CEFについて、CEを底辺と考えると、三角形CEFは平行四辺形ABCD（100 c㎡）に比べて、底辺は6cm÷10cm＝3/5（５分の３）、高さは8cm÷12cm＝2/3（３分の２）、さらに三角形なので1/2（２分の１）となる。よって、三角形CEFの面積は、100c㎡×3/5×2/3×1/2 ＝ 20c㎡。